A Basic Slicer for 3D Printing

CNC machines, like fused deposition modeling (FDM) 3D printers, rely on G-code instructions to fabricate objects. In the case of 3D printing, slicer programs take 3D models, usually stored with the STL file extension, and generate G-code that can be given to the printer. At its core, this process of slicing objects is actually a simple algorithm. To slice an object for printing, we only need to take evenly spaced contours in the vertical direction, producing several cross-sections (AKA slices). Following this, we produce infill within each of these contour curves. For this project, a rectilinear infill was implemented, which only draws evenly spaced parallel lines within each slice. Once these slices are generated, they are broken down into small movements in the XY plane to draw the curves. To go to the next layer and print that slice, we write a G-code instruction that raises the extruder by the layer height.

Materials

The MK3 Prusa 3D printers in the BTU Lab were used for this project. The prints were fabricated with generic PLA filament.

Creating Perimeters and Infill in Grasshopper

Below are some images of the Grasshopper script for creating a basic cylinder and slicing it.

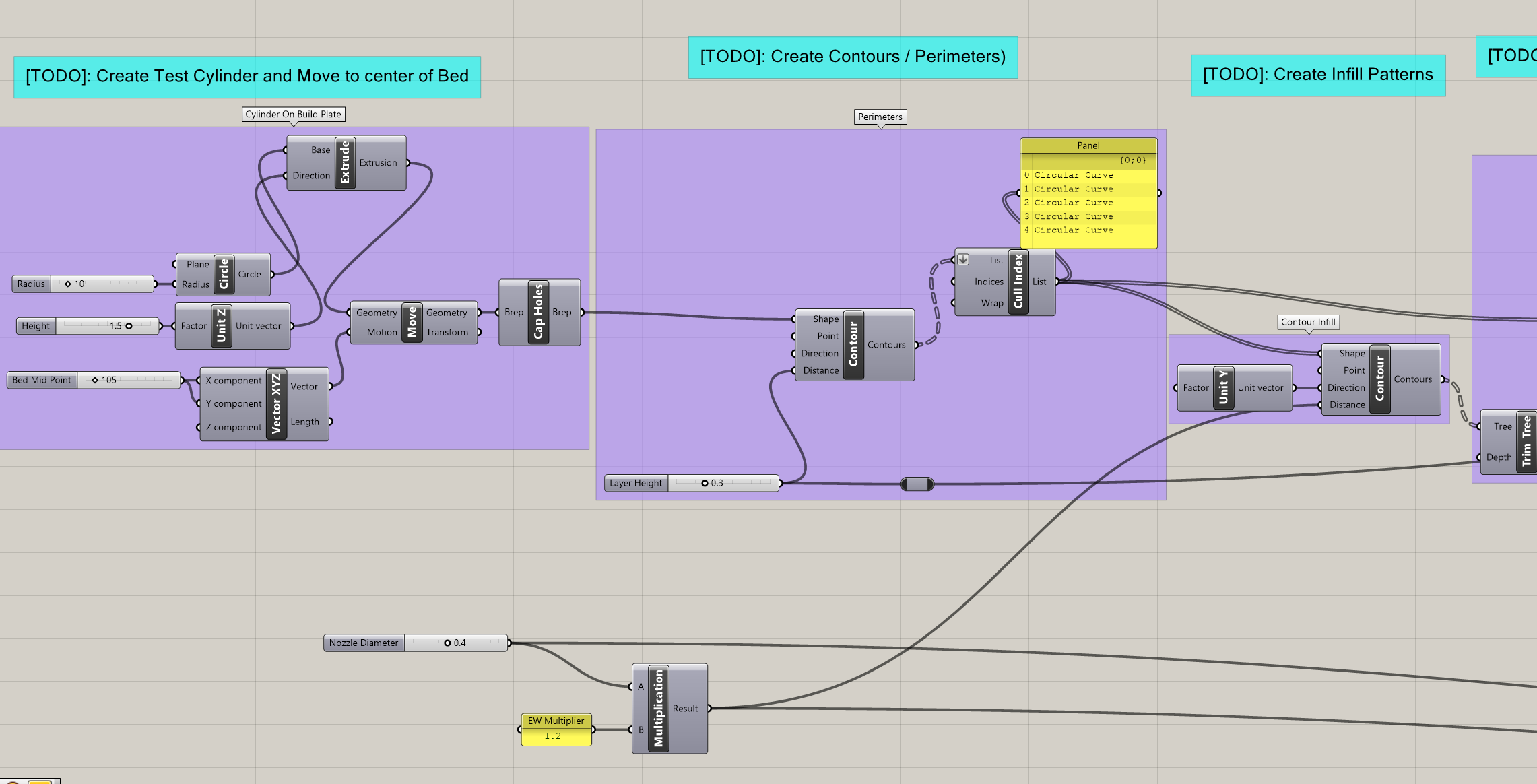
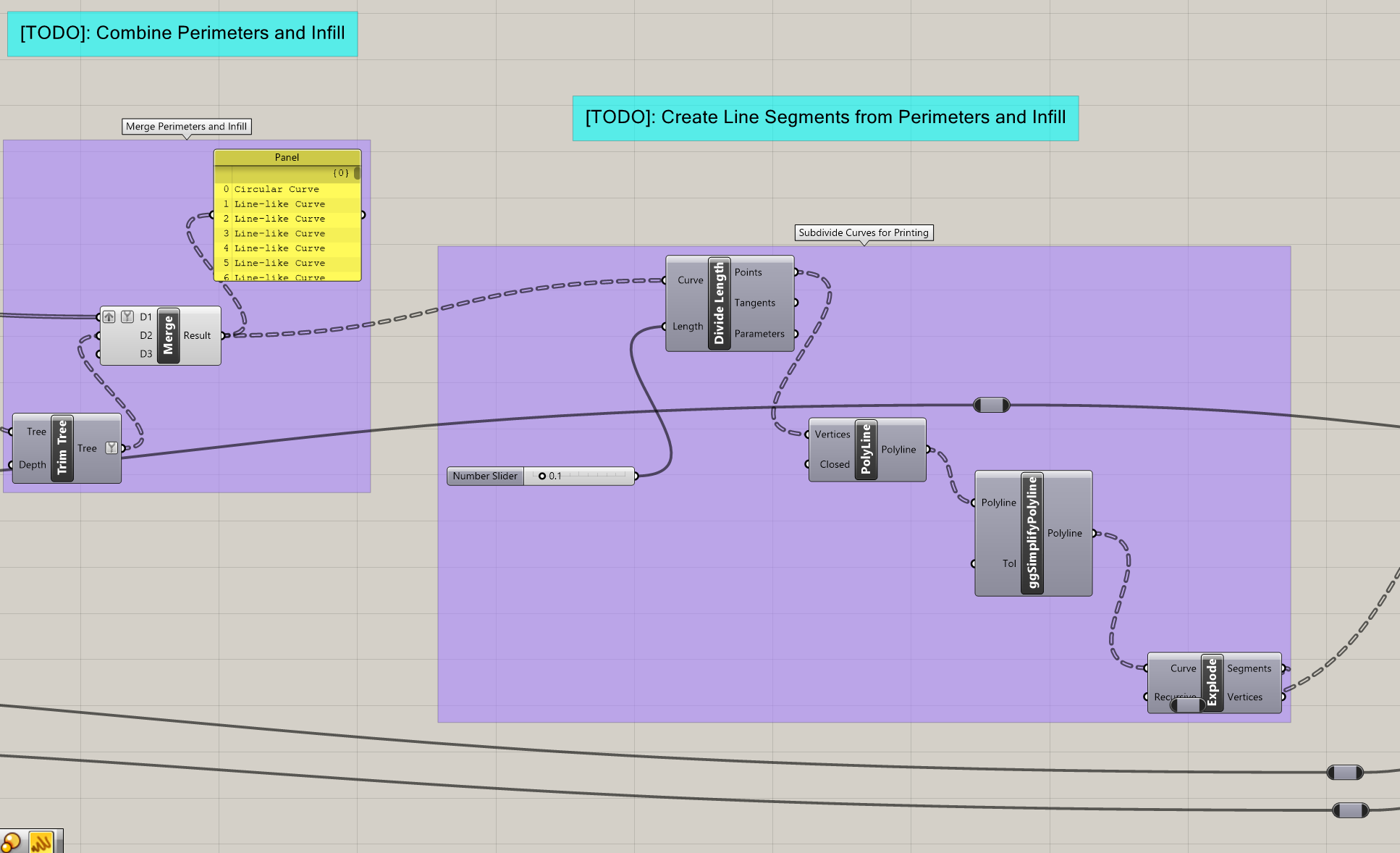
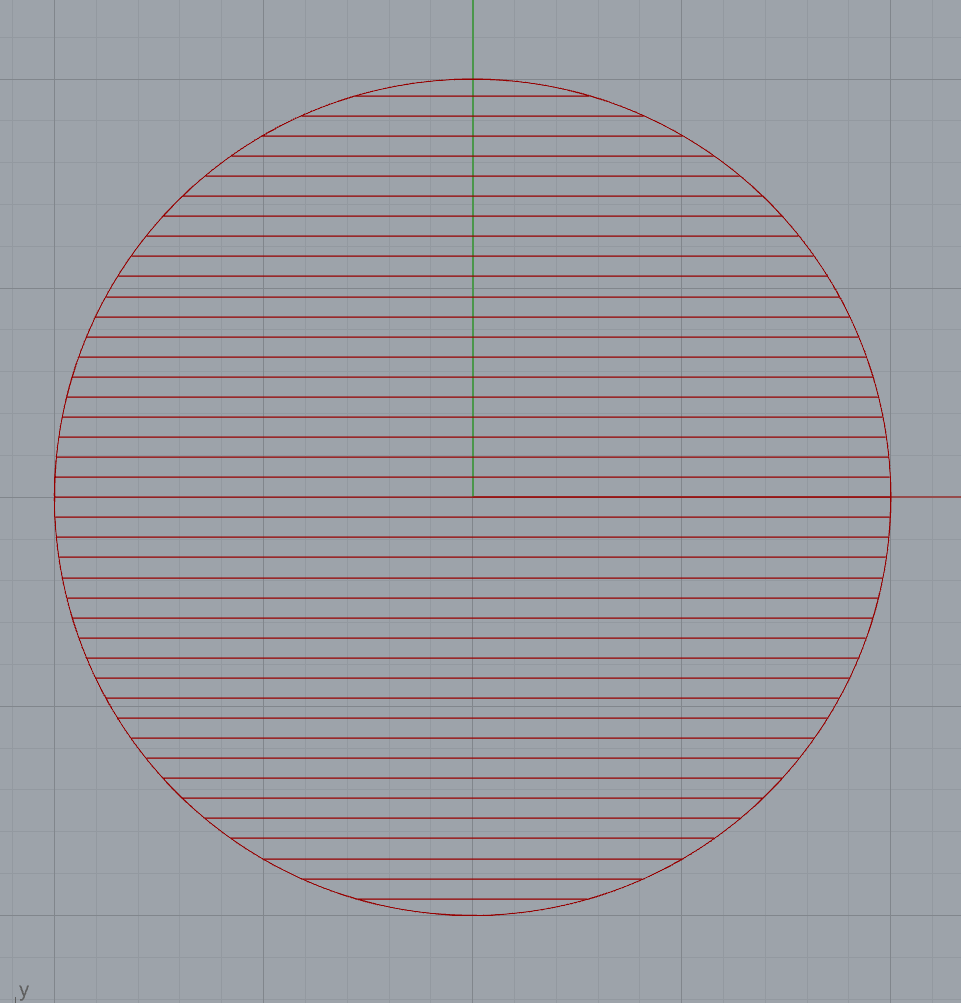
Below are examples of the resulting slices, complete with rectilinear infill.

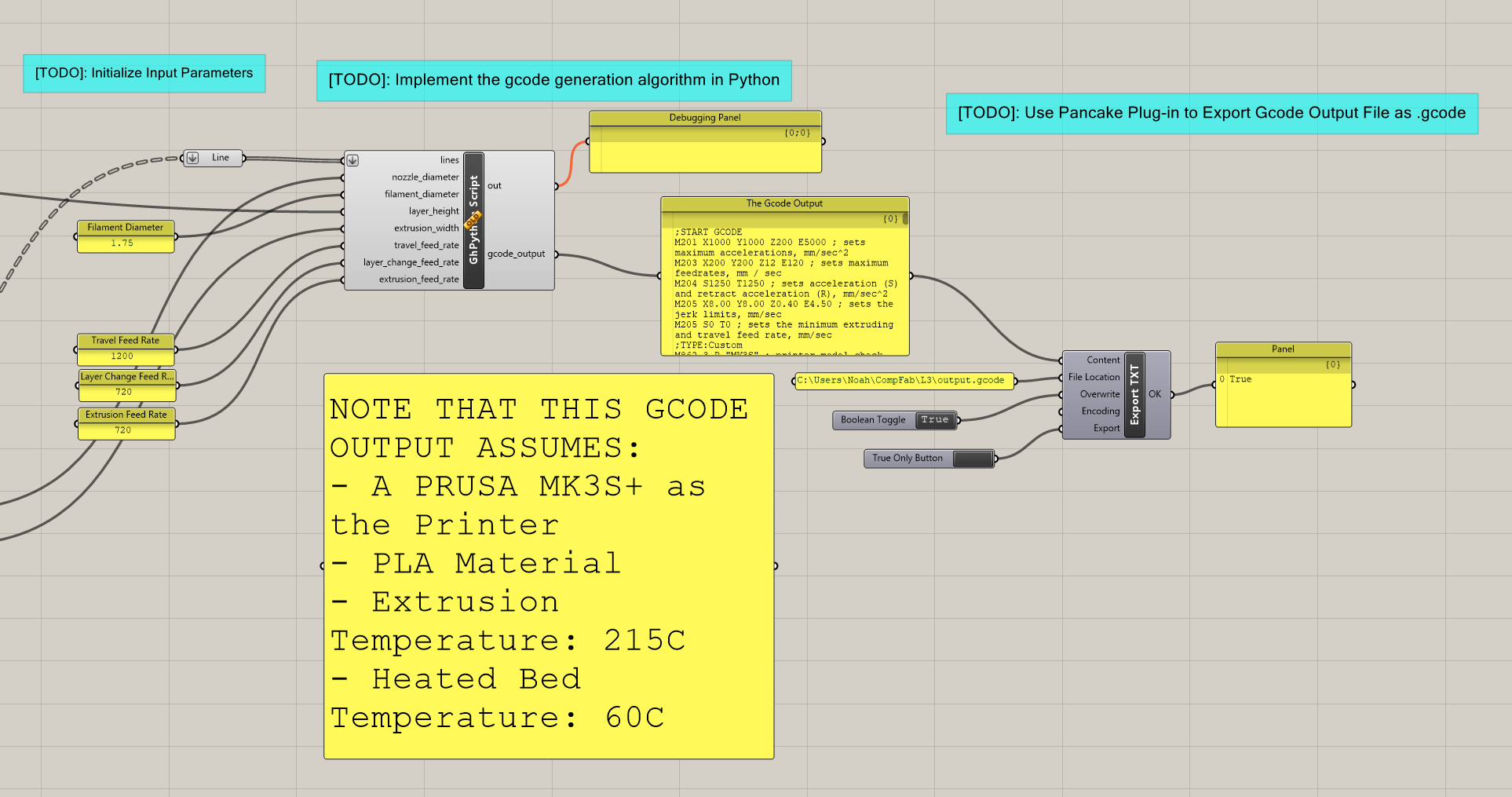
G-Code Generation

As can be seen from the Grasshopper script above, the line segments from the sliced object are sent to a Python script that generates G-code for the printing process. The full script, most of which was provided by Professor Michael Rivera, is shown below.

This script’s accuracy was verified by checking its output in the Zupfe Gcode Viewer.

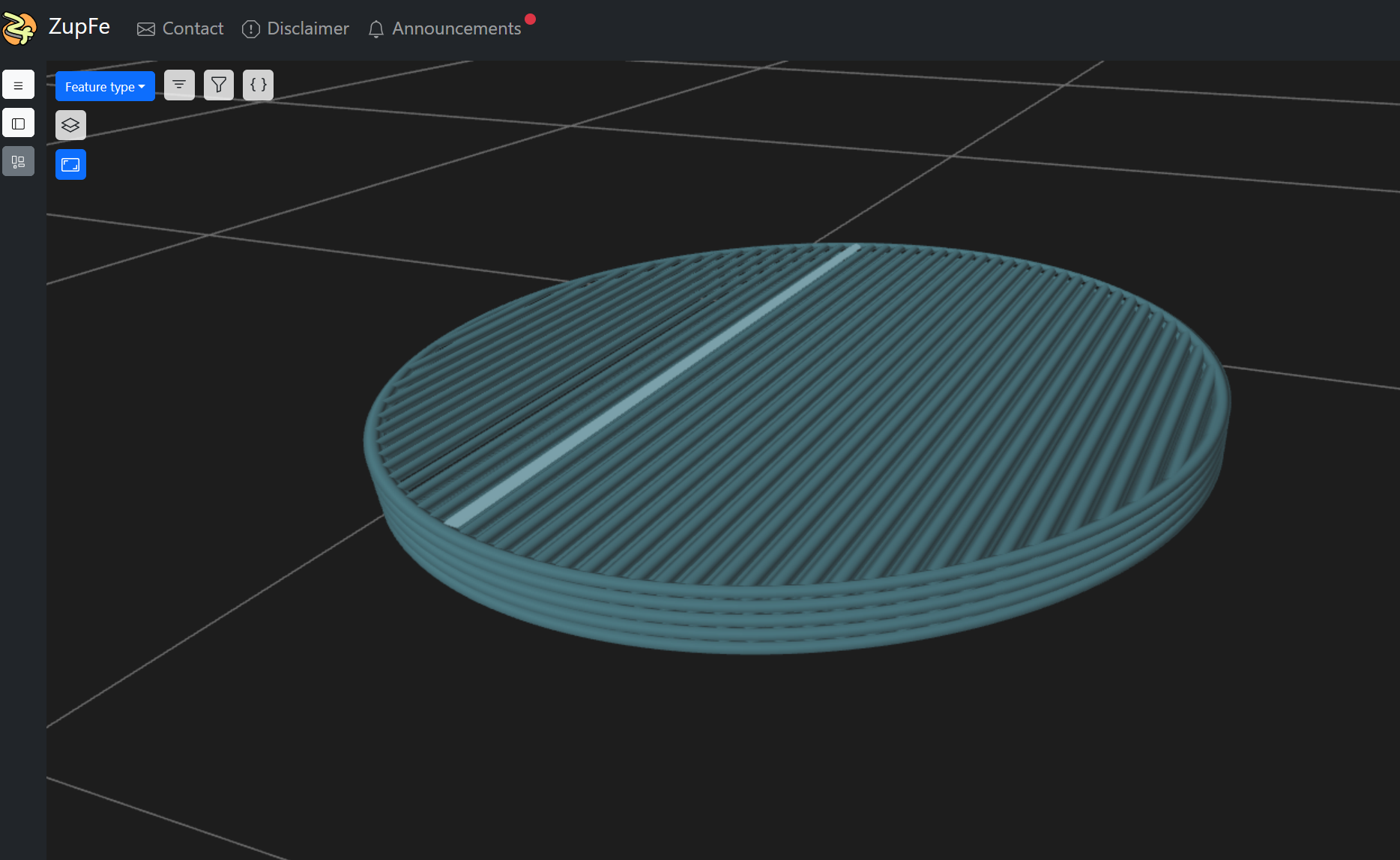
The G-code output also passed the course validator tool, as seen below.

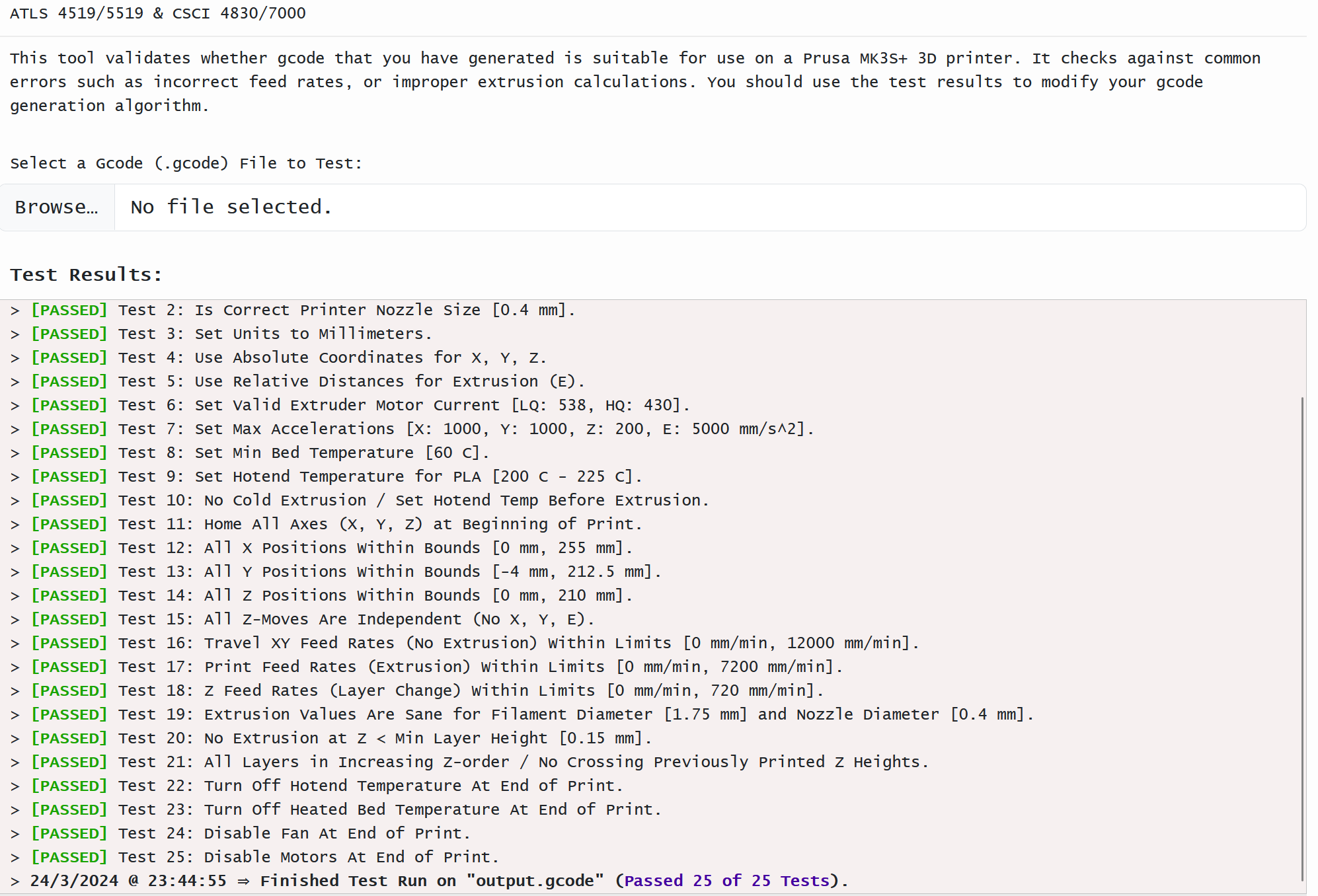
Download the full G-code file here.

Print Results

See the resulting cylinder prints below. Each cylinder’s height is 1.5 mm, resulting in 5 0.3 mm layers. The cylinders have the same radius as well. The first cylinder (on the left) was printed by slicing an STL file using the Prusa Slicer. The second cylinder, on the right, was printed using my generated G-code instructions.

Conclusions

The main difference I noticed between the 2 prints was the time. The reason is simple enough, as the first cylinder only used 15% infill, whereas my implementation used 100% infill, putting the parallel lines of the rectilinear infill as close as possible. The first print took about 5 minutes, and the second took 10.

You can see the tighter infill in the second cylinder from the top view. From the side, there aren’t any apparent differences between the two prints, which indicates that my G-code generator was successful, at least for a simple object like this tiny cylinder.